1. K取不同值时带来的影响
举例:
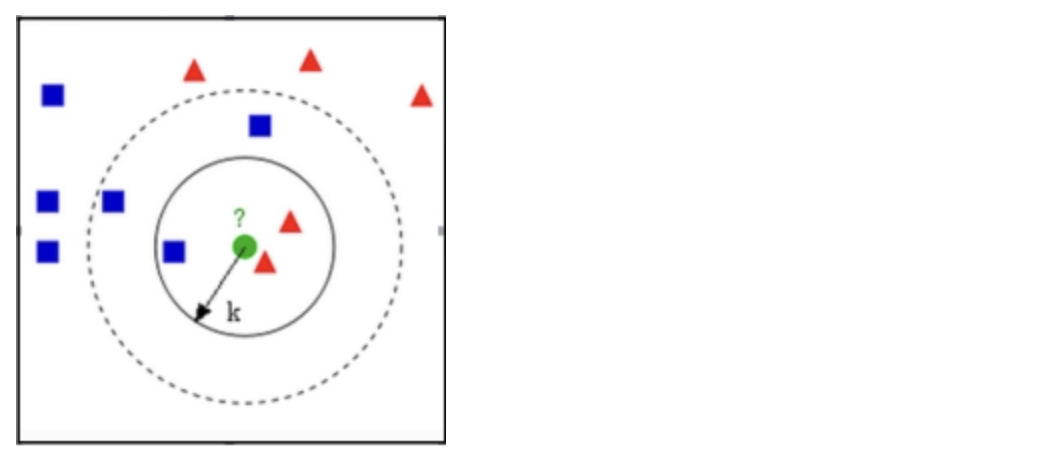
- 有两类不同的样本数据,分别用蓝颜色的小正方形和红色的小三角形表示,而图正中间有一个绿色的待判样本。
- 问题:如何给这个绿色的圆分类?是判断为蓝色的小正方形还是红色的小三角形?
- 方法:应用KNN找绿色的邻居,但一次性看多少个邻居呢(K取几合适)?

解决方案:
- K=4,绿色圆圈最近的4个邻居,3红色和1个蓝,按少数服从多数,判定绿色样本与红色三角形属于同一类别
- K=9,绿色圆圈最近的9个邻居,6红和3个蓝,判定绿色属于红色的三角形一类。
有时候出现K值选择困难的问题
KNN算法的关键是什么?
答案一定是K值的选择,下图中K=3,属于红色三角形,K=5属于蓝色的正方形。这个时候就是K选择困难的时候。
2. 如何确定合适的K值
K值过小:容易受到异常点的影响
k值过大:受到样本均衡的问题
K=N(N为训练样本个数):结果只取决于数据集中不同类别数量占比,得到的结果一定是占比高的类别,此时模型过于简单,忽略了训练实例中大量有用信息。
在实际应用中,K一般取一个较小的数值
我们可以采用交叉验证法(把训练数据再分成:训练集和验证集)来选择最优的K值。
3. GridSearchCV 的用法
使用 scikit-learn 提供的 GridSearchCV 工具, 配合交叉验证法可以搜索参数组合.
# 1. 加载数据集
x, y = load_iris(return_X_y=True)
# 2. 分割数据集
x_train, x_test, y_train, y_test = \
train_test_split(x, y, test_size=0.2, stratify=y, random_state=0)
# 3. 创建网格搜索对象
estimator = KNeighborsClassifier()
param_grid = {'n_neighbors': [1, 3, 5, 7]}
estimator = GridSearchCV(estimator, param_grid=param_grid, cv=5, verbose=0)
estimator.fit(x_train, y_train)
# 4. 打印最优参数
print('最优参数组合:', estimator.best_params_, '最好得分:', estimator.best_score_)
# 4. 测试集评估模型
print('测试集准确率:', estimator.score(x_test, y_test))
4. 小结
KNN 算法中K值过大、过小都不好, 一般会取一个较小的值
GridSearchCV 工具可以用来寻找最优的模型超参数,可以用来做KNN中K值的选择
K近邻算法的优缺点:
- 优点:简单,易于理解,容易实现
- 缺点:算法复杂度高,结果对K取值敏感,容易受数据分布影响